Snow Forecast


Snow Camera - Top of Valley


Snow Depth Prediction 2025

by Bruce A. Peterson

The maximum depth of the winter snow in the Australian Alps varies from year to year. If these variations were random, then the best guess for next year's maximum snow depth would be the average depth. If a linear trend and some cyclical factors are present, then it should be possible to quantify these, and make a better guess. However see the Trend Analysis, especially the final paragraph.

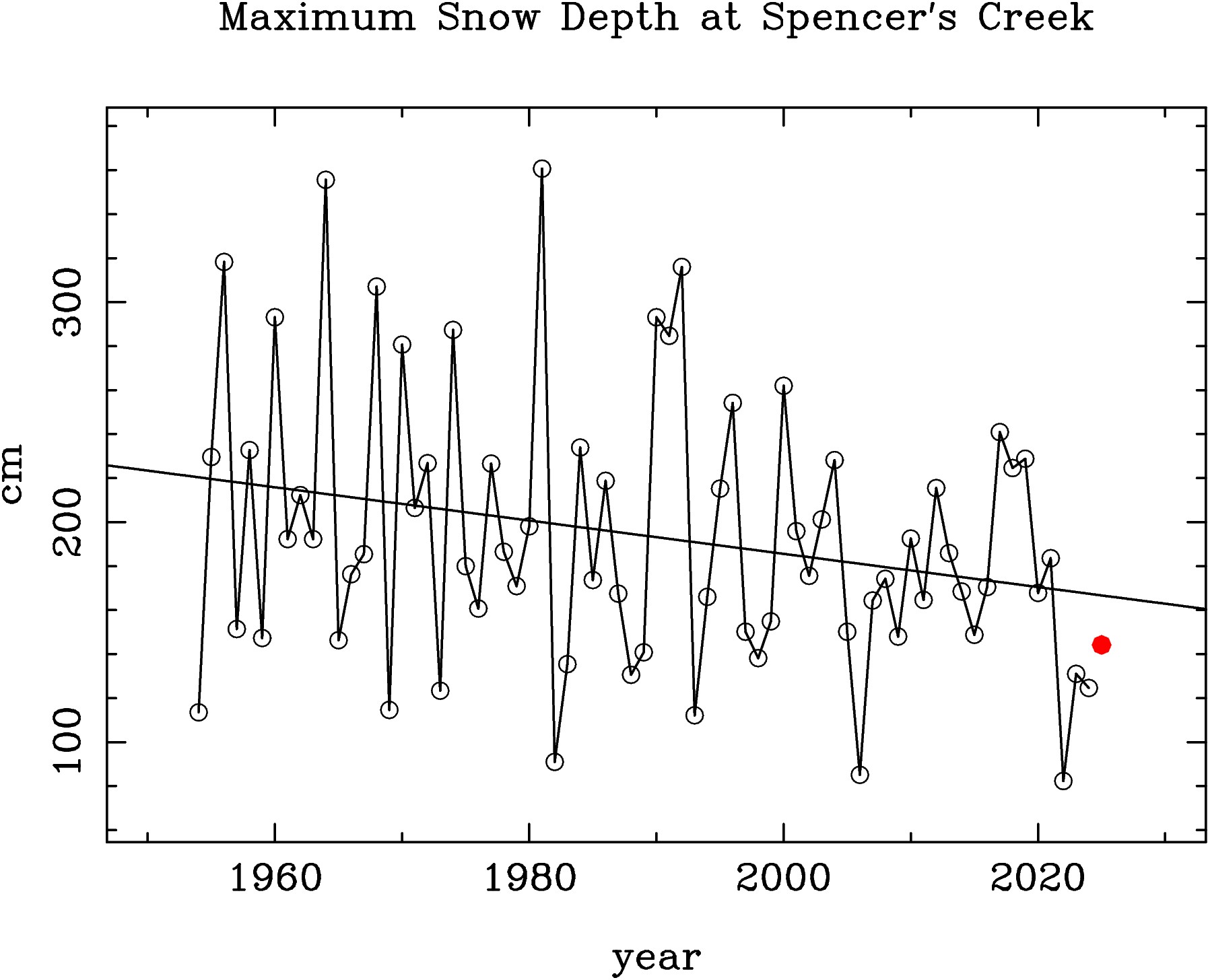
Figure 1. -- Maximum snow depth for each year (open circles joined by line) as measured by the Snowy Mountains Hydro-Electric Authority at Spencer's Creek in the Australian Alps, and the predicted 2025 maximum snow depth using maximum entropy and linear prediction (red filled circle). The sloping line represents the linear least squares fit to the measured snow depths.

From inspection of Figure 1, it appears that an exceptionally good year is often (but not always) followed by several poor years, and that there appears to be a systematic decrease in snow depth with time. I have analyzed the year to year fluctuations assuming that, in addition to a purely random component, there are periodic components which can be derived from the historical measurements, and that these can be used to predict future behavior. In addition to random fluctuations, a decrease of 7.6 cm/decade and cyclic components with periods of about 4 years were found, and used to predict the maximum snow depth for next year.

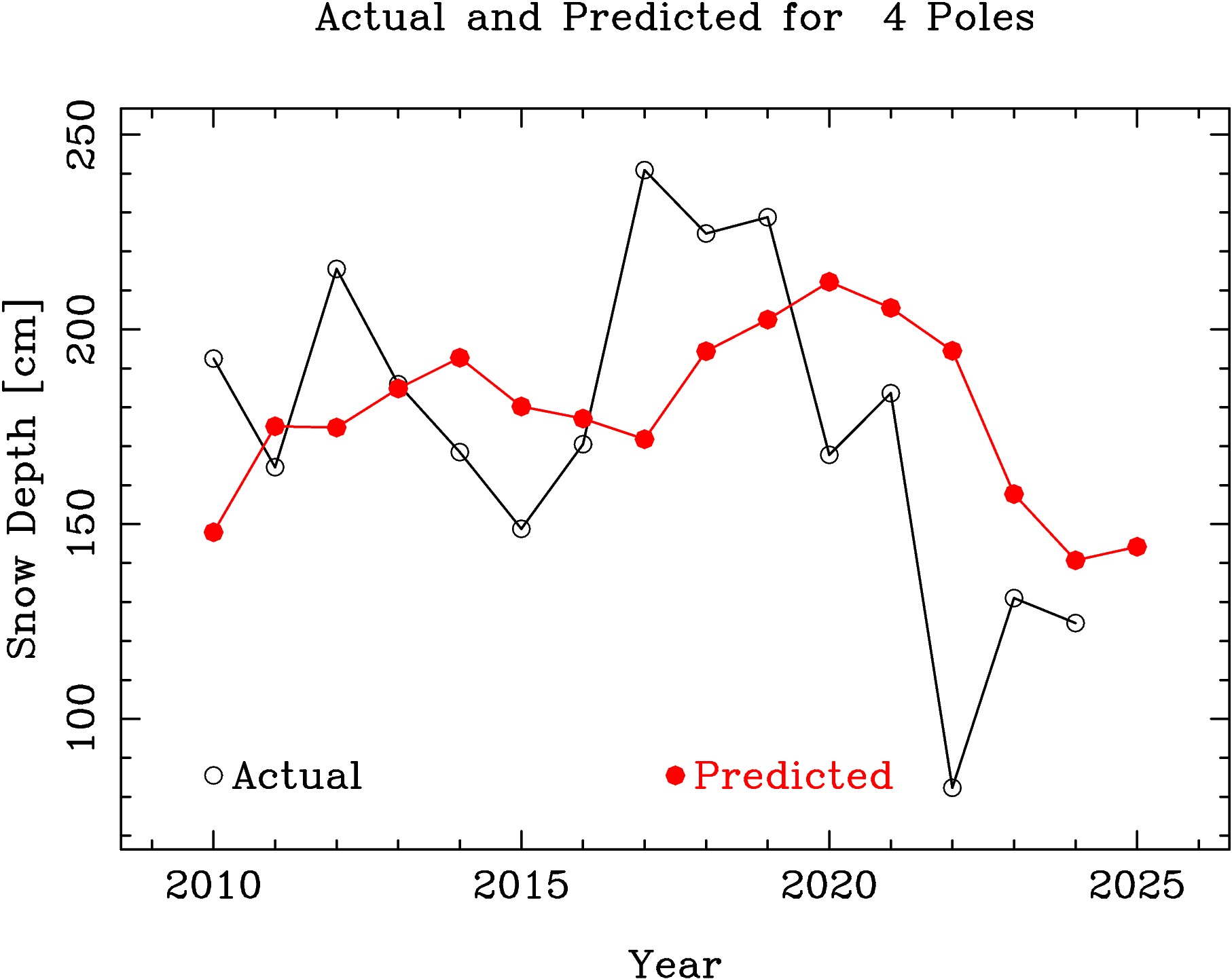
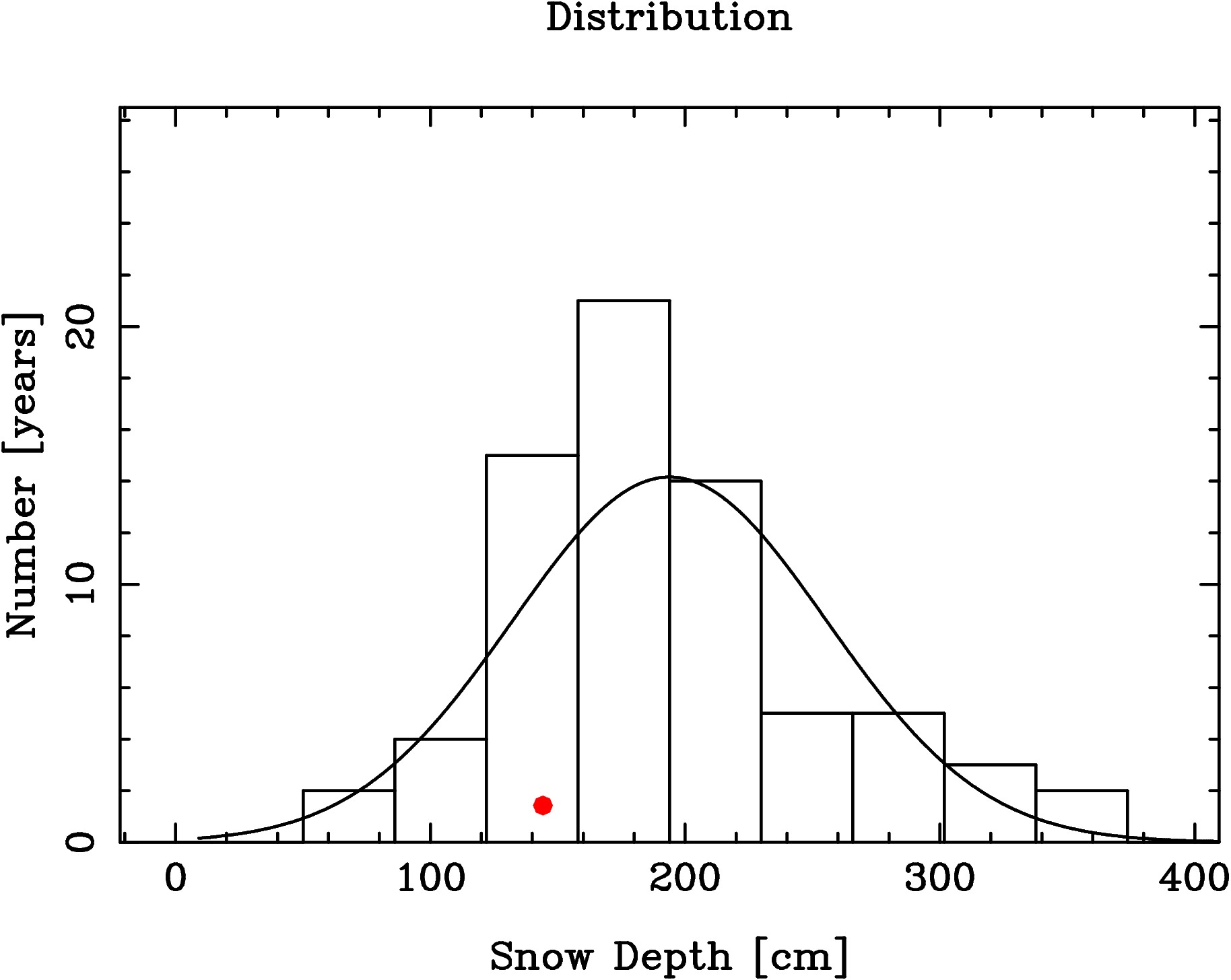Figure 2. -- Distribution of maximum snow depths. Actual values are represented by the solid line histogram. For comparison, a random distribution with the same average value and variance is represented by the curved line. The predicted 2025 value is shown as a red filled circle.

As can be seen in Figure 2, years with below average snow depths occur more often than expected from purely random variations, as do exceptional years with depths exceeding the average by more than 100 cm.

The prediction for 2025, based on the measurements from 1954 through 2024, is for a maximum snow depth of 144.2 cm, which is 49.7 cm less than the 71 year average of 193.9 cm, 22.5 cm less than the 166.7 cm expected from the decreasing linear trend, and 19.6 cm above the actual 124.6 cm in 2024.

We can expect the 2025 snow depth to be below the long term average, slightly below the liner trend, and slightly better than last year.

I computed the maximum entropy and linear prediction values made with a varying number of poles, and found that the minimum of root-mean-square differences between the predicted and actual values was obtained using only 4 or 5 poles.

Figure 3. -- A Comparison of Predicted and Actual Snow Depths. Each prediction uses all of the historical data up to, but not including, the year being predicted. The actual depth is that measured for the year being predicted.

Trend Analysis

Figure 4. -- Maximum snow depth for each year (open circles joined by line)as measured by the Snowy Mountains Hydro-Electric Authority at Spencer's Creek in the Australian Alps. The sloping line represents the linear least squares fit to the measured snow depths.

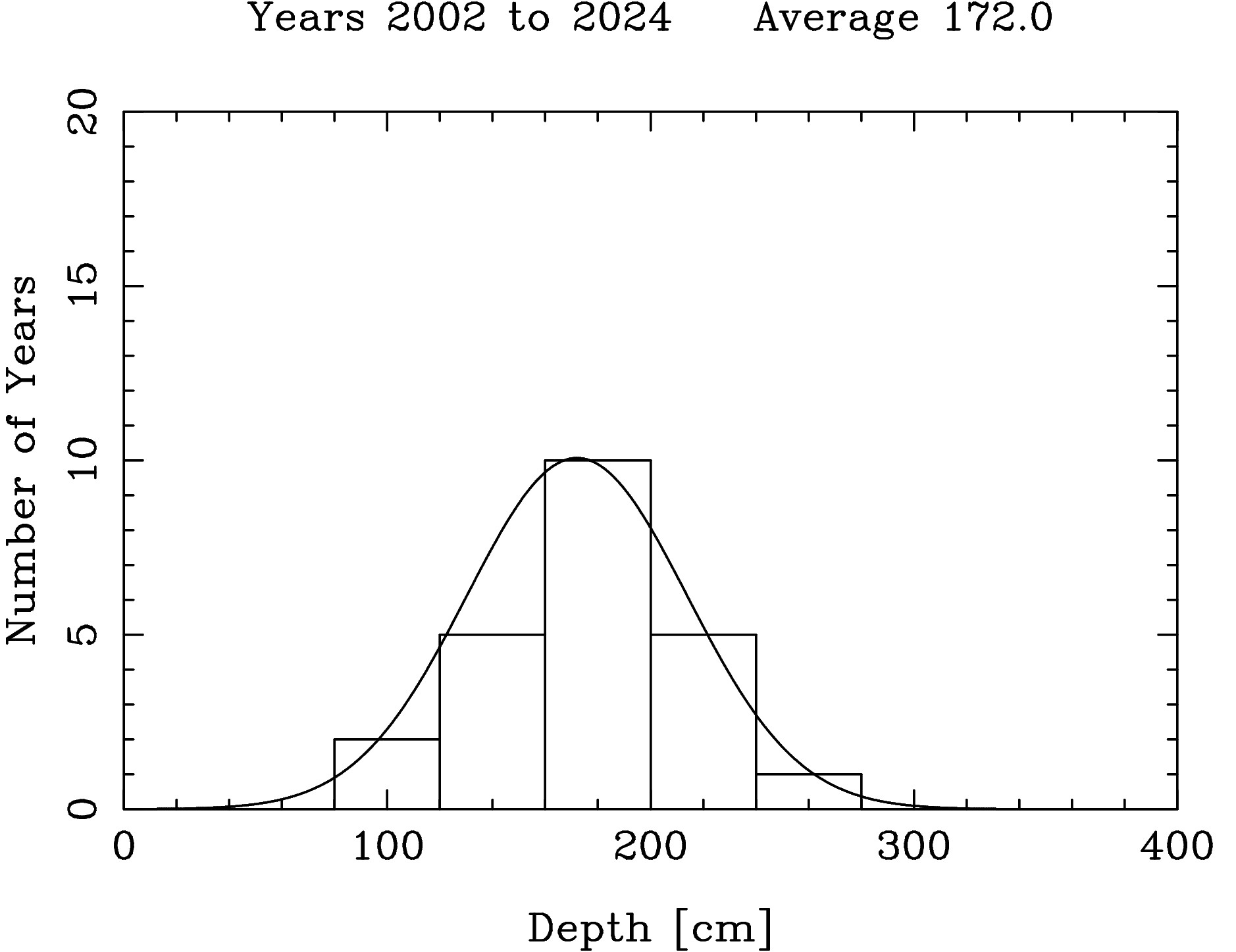
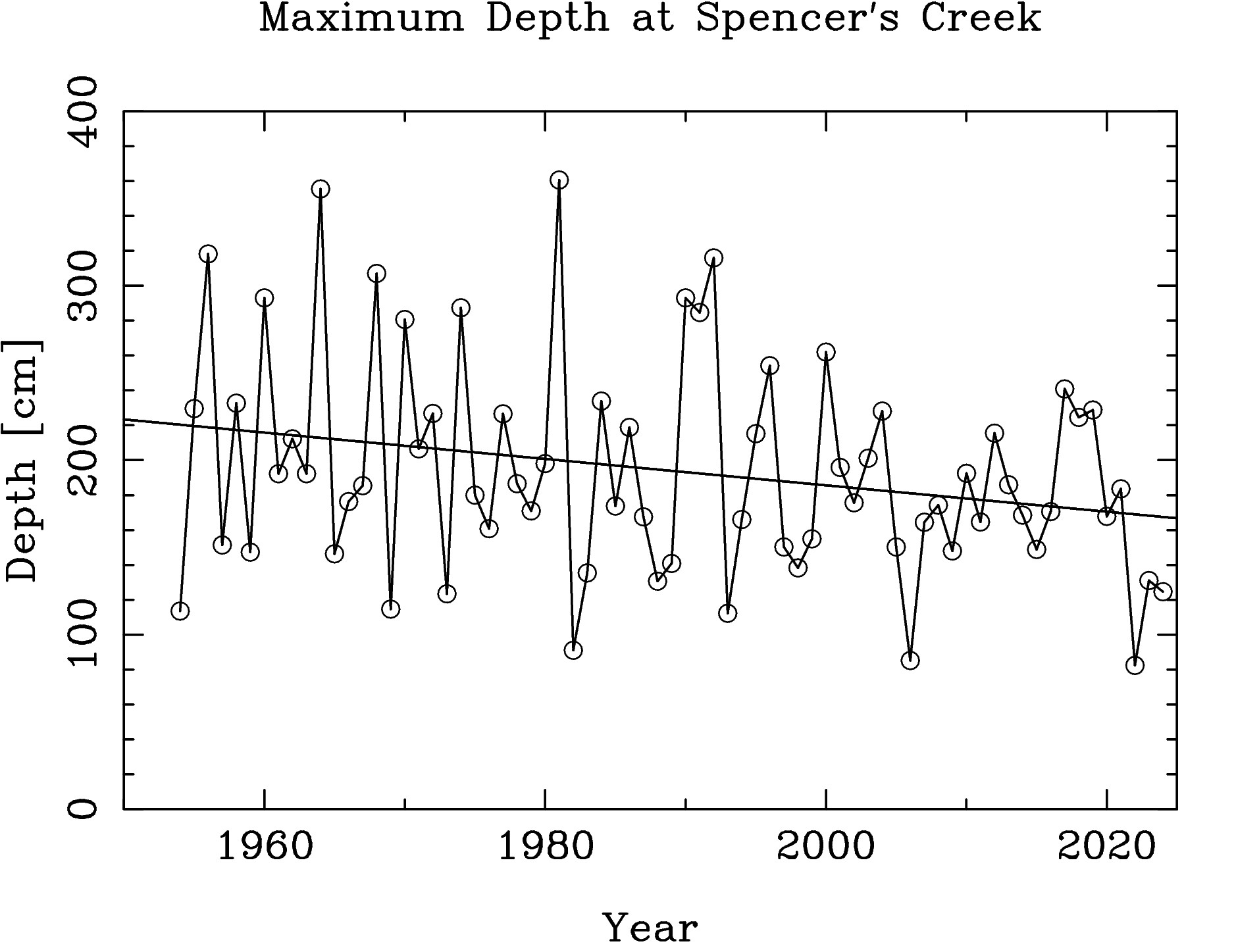The line has a slope of 7.6 cm/decade. With a probable error of 3.5 cm/decade.

The data were divided into three periods, plots made of the snow depth distributions for each period, and some statistics calculated from the data of each period.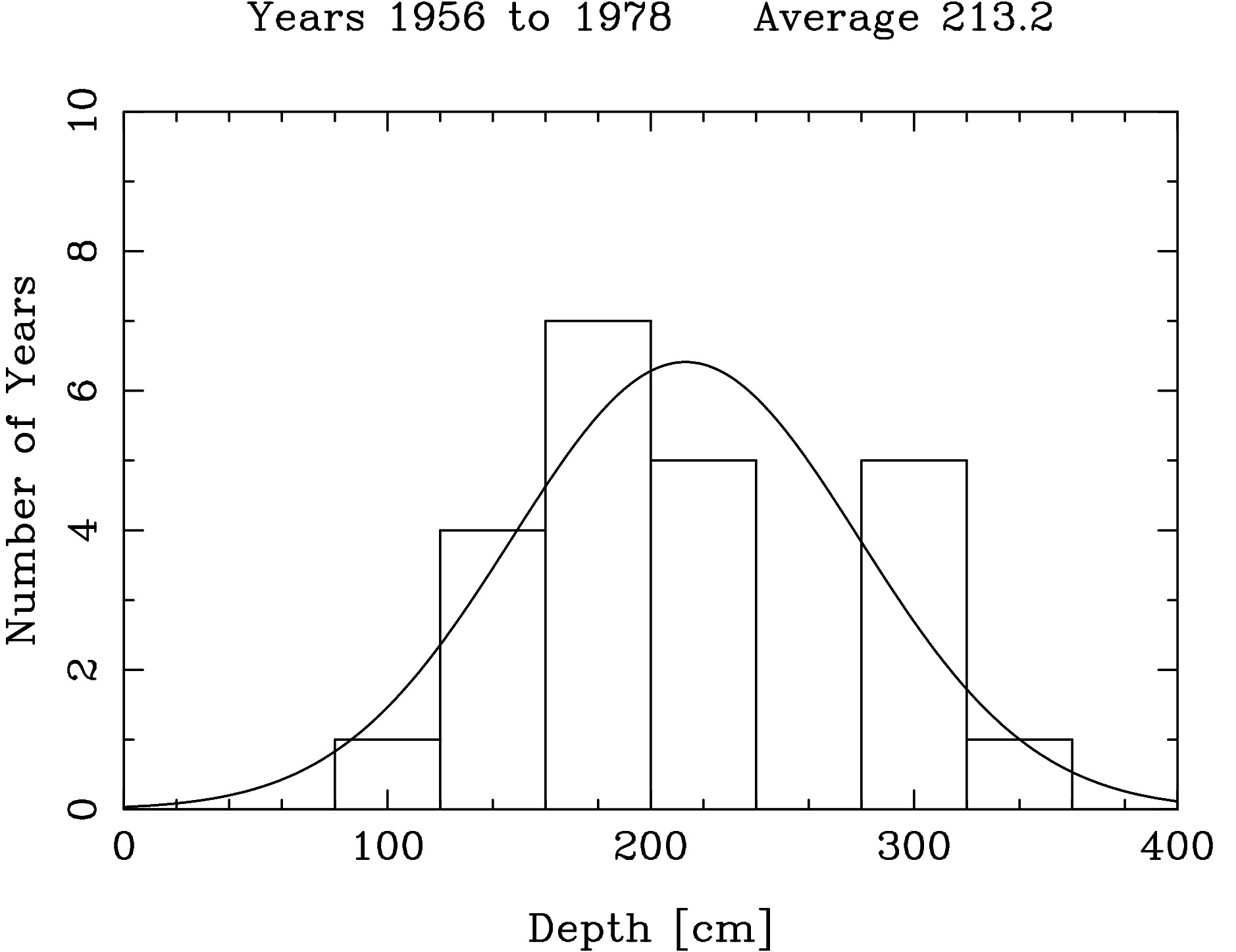

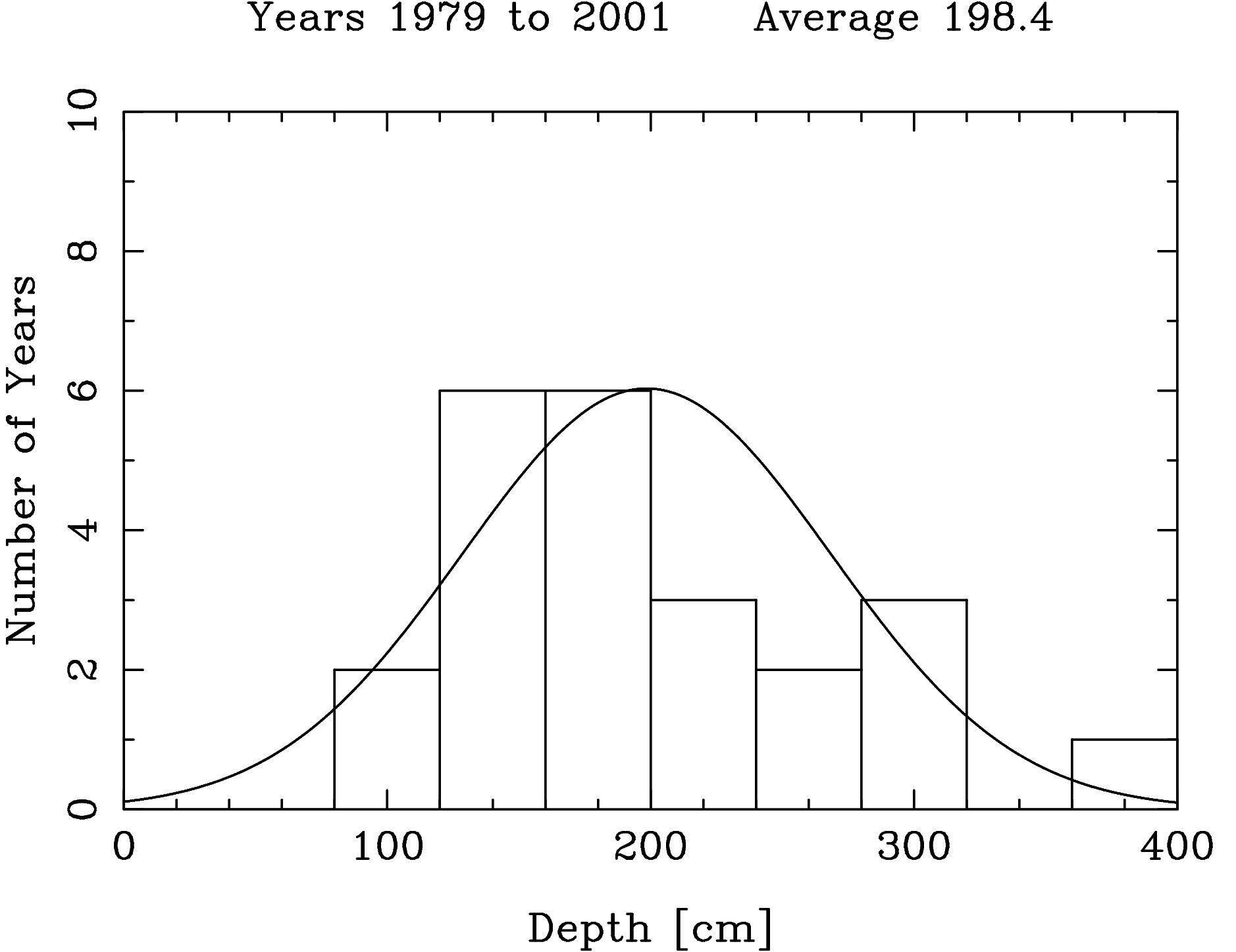
Figure 5. -- Distribution of maximum snow depths for the 23 year periods 1956-1978, 1979-2001, and 2002-2024. Actual values are represented by the solid line histogram. For comparison, a random distribution with the same average value and variance is represented by the curved line.

Note that the first two periods ( 1956-1978 and 1979-2001) have an excess of years with high snowdepths, while the latest period ( 2002-2024) has a more random distribution of snowdepths peaked at 172.0 cm, and a smaller variance of 41.9 cm

Snow Depth Trends

(1) (2) (3) (4) (5) (6)
Average Variance Median 2-3 meters > 3 meters
Years cm cm cm N % N %
1956-1978 213.2 65.8 192.3 8 35 3 13
1979-2001 198.4 70.0 173.7 7 30 2 9
2002-2024 172.0 41.9 170.5 6 26 0 0

Column 5 gives the number of years, and the percentage of years, in the interval given in Column 1, where the maximum snow depth was between 2 and 3 meters. Column 6 gives the number of years, and the percentage of years, in the interval given in Column 1, where the maximum snow depth was above 3 meters. Fewer years had maximum snow depths above 3 meters in the later periods, leading to a drop in the average and median depths, as well as to a smaller spread in depths about the average. This can be seen in the plots of the distributions as well as in the above table.

The Kolmogorov-Smirnov Test is used to obtain the probability that two data samples are drawn from the same underlying distribution.

First, I compare the distribution of measured snow depths with a normal distribution with the same average and variance as that found for all the snow depth data. This probability is inversely related to the maximum vertical separation between the two lines in Figure 6.

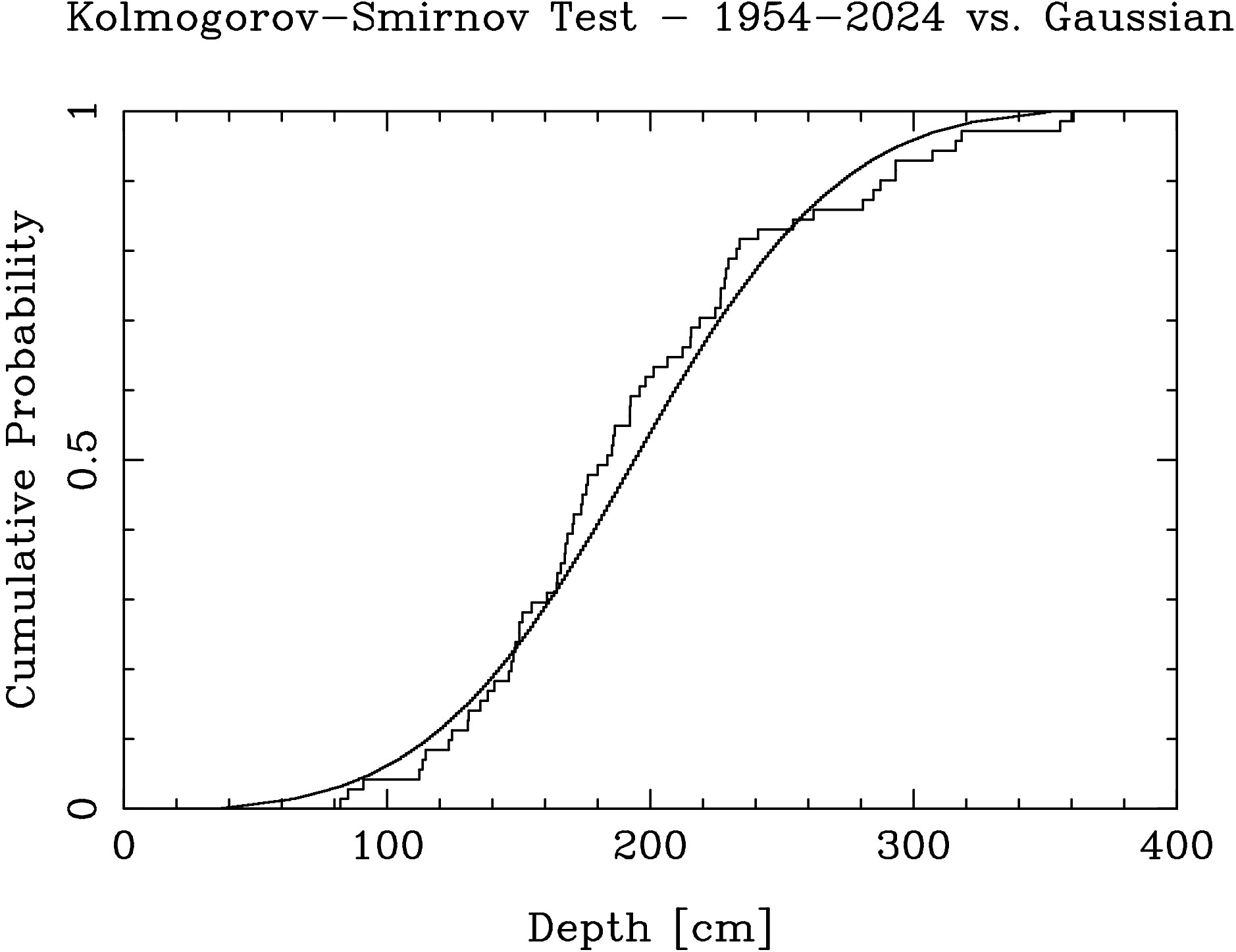
Figure 6. -- Kolmogorov-Smirnov Test comparing cumulative probability for snow depths (stepped line) with a normal distribution (smooth curve) having the same average and variance.

The result of the Kolmogorov-Smirnov Test is that there is 50.4% probability that the snow depth distribution from 1954 through 2024 represents a random distribution with average 193.9 and a standard deviation of 48.5 with no linear trend.

However, there is a clear difference between the early data and more recent data, as seen in Figure 5 and the table of Snow Depth Trends.

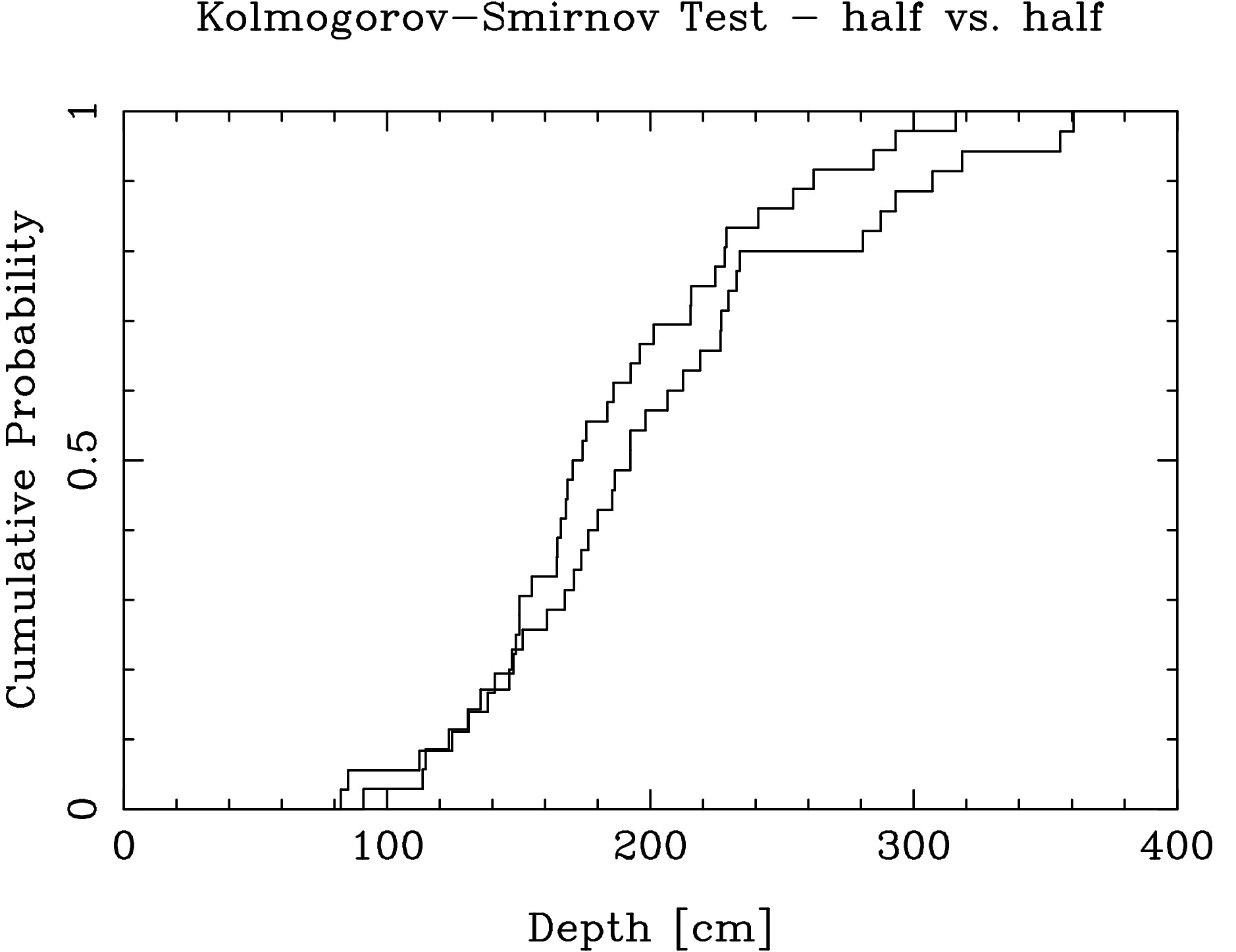Figure 7. -- Kolmogorov-Smirnov Test comparing cumulative probability for snow depths from 1954-1987 with snow depths from 1988-2024

The result of this second Kolmogorov-Smirnov Test is that there is a 52% probability that the snow depth distribution from 1955-1989 comes from the same underlying distribution as the snow depth distribution from 1990-2024.

The snow depth of the last 10 years has an average of 170.3 cm and a variance of 48.4 cm, as compared to the snow depth of the past 23 years, given in the table Snow Depth Trends, which has an average of 172.0 cm and a variance of 41.9 cm. I expect that snow depth for 2025 will not be much different than the average of the last 10 years, 170.3 cm, and perhaps only slightly lower than the linear trend, and higher than last year.

contact: Bruce A. Peterson 37717th access Last modified: Fri 2 May 2025